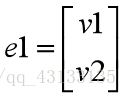图论
七桥问题
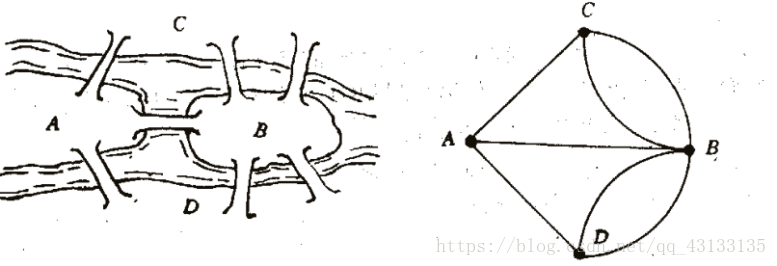
有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸联系起来(如概述图)。有个人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七
座桥,最后回到出发点?
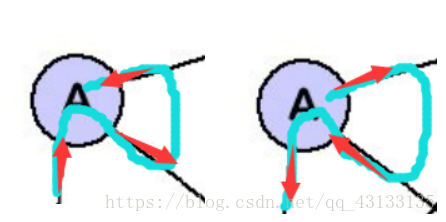
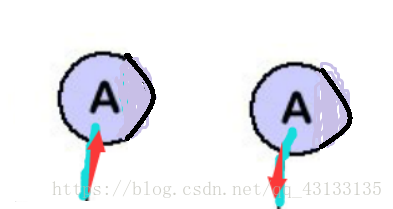
偶数边节点等效为如下一进一出的两条边节点
该节点必然是一笔画的起点(右图形式)或者终点(左图形式)
A、C、D、B节点均为奇数边
故等效为4个起始点,而一个一笔画的图最多只能有两个起始点。
PS:若要求一笔画的终点和起点重合, 全为偶数边`,这就是十分显然的了
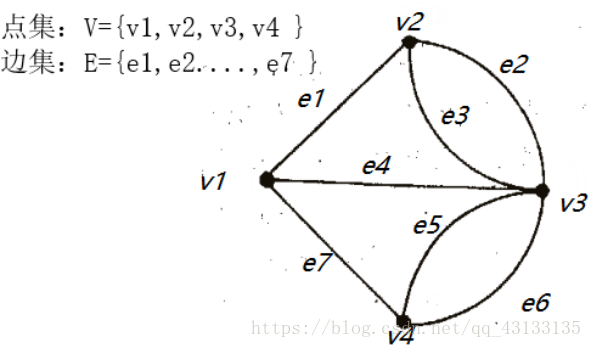
图的表示分为两块
1、节点
2、边
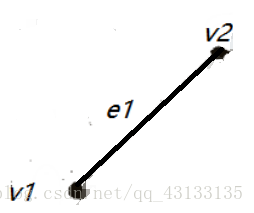
对于任意某条边,以边e1为例:
由于任意边节点只有两个,我们不妨记为
以节点\边 的矩阵表示:
| \ | e1 | e2 | e3 | e4 | e5 | e6 | e7 |
|---|---|---|---|---|---|---|---|
| V1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| V2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| V3 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| V4 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
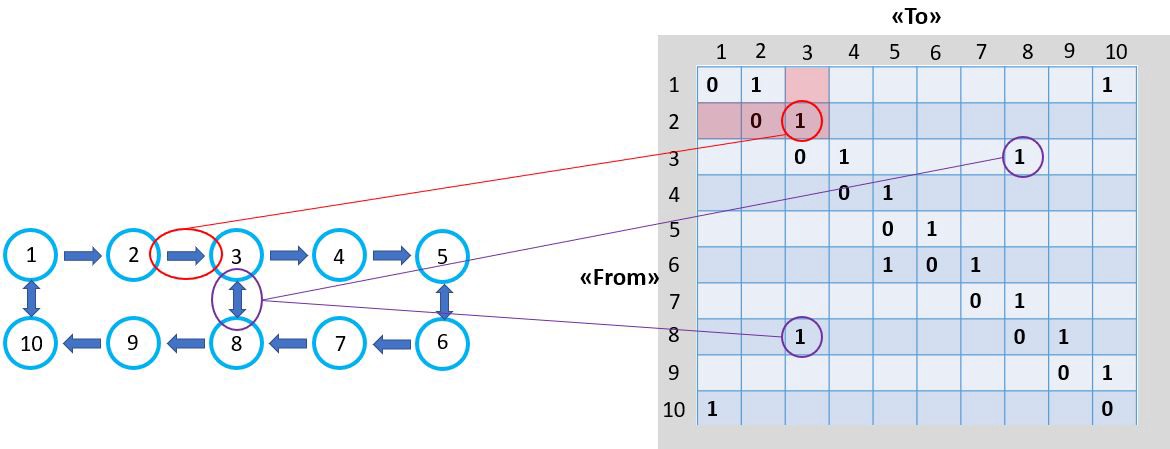
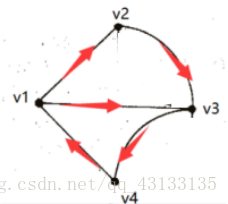
FROM/TO 方向矩阵表示:
| \ | V1 | V2 | V3 | V4 |
|---|---|---|---|---|
| V1 | 0 | 1 | 1 | 0 |
| V2 | 0 | 0 | 1 | 0 |
| V3 | 0 | 0 | 0 | 1 |
| V4 | 1 | 0 | 0 | 0 |
实际问题
拣货问题:
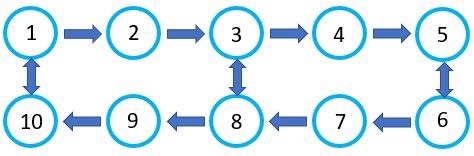
下图显示了2条走廊,每个走廊有5个搁板/拾取点。 在此,所有架子都表示为图中的节点,地址范围为1-10。 箭头指示允许的行驶方向,双箭头指示您可以两种方式行驶。 很简单,对不对?1->9 最近的路线?